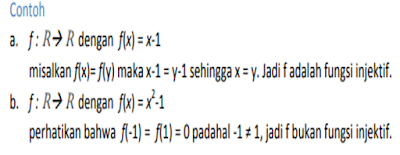Grafik Turunan

Assalamu'alaikum!

Cara membuat grafik dari turunan

=> Turunkan terlebih dahulu

=> Usahakan harus berbentuk faktor diakhir sehinga mudah dicari akar-akar x nya

Setelah semua titik sudah didapatkan, buat Interval naik turunnya, dengan menguji titik pada f '(x).

Gambar diatas ini untuk mencari ketinggian dari gambar grafik, saya coba di titik X=-1 pada fungsi awal mula sehingga gambar grafik seperti dibawah ini

Semoga bermanfaat sekian

Mohon maaf bila banyak kekurangan, baik tulisan hingga gambar.

Wassalamu'alaikum :D

Limit Tak Tentu 0^0 / ∞^0 / 1^∞

Assalamu'alaikum !

bagaimana jika kita menghadapi soal yang hasilnya seperti Limit tak tentu diatas ?

cukup kita ubah bentuknya saja menggunakan ln dan turunan l'hopital didalamnya, seperti contoh berikut,



Jadi paham kan ? :D
setelah kita ubah ruas kanan dan kiri kedalam bentuk "ln" jangn lupa diakhirnya dikembalikan ke bentuk asal yaa :D

Kurangnya mohon dimaafkan Wassalamu'alaikum

Limit Tak Tentu 0/0 , ∞/∞

Assalamu'alaikum !

Bagaimana cara menghadapi soal yang hasilnya bentuk tak tentu ?
Pakai dalil l'hopital

Jika ada yang ingin didiskusikan silahkan :)
Sekian Wassalamu'alaikum :D

Turunan Implisit, Turunan Kedua, Turunan Eksponen Asli

Assalamu'alaikum !

Ada sedikit materi mengenai Turunan Fungsi Implisit, Turunan Kedua Fungsi, dan Turunan Fungsi Eksponen Asli

Langsung gas











Semoga dapat mudah dimengerti, jika ingin mengetahui langkah menurunkannya silahkan cek di youtube Link : (proses)

Jika ada kesalahan atau pertanyaan, bisa kita diskusikan bersama dikolom komentar :)
Kurangnya mohon dimaafkan, Wassalamu'alaikum :)

Turunan Fungsi

Assalamu'alaikum!











Begitulah beberapa jenis turunan fungsi

Mohon maaf bila ada kesalahan dan banyak kekurangan
Wassalamu'alaikum

#Nb: Komentari perbaikan dari kesalahan yaa :D

Grafik Turunan Lanjutan

Assalamu'alaikum!

Pada postingan kali ini, akan membahas langkah-langkah mengerjakan grafik turunan

1. Cari Turunan pertama dari soal (f'(x)).



2. Cari Turunan kedua (f''(x)). Tentukan titik kritis dan interval naik/turunnya.

 

3. Cari titik belok cekungnya.



4. Uji Nilai Ekstrim dan Gambar Grafiknya.



Jika anda membuat titik x lebih banyak dan dimasukkan kepersamaan f(x), akan mendapatkan nilai-nilai untuk kerapihan gambar, sepertdi gambar diatas yang hanya menggunakan 3 titik, yakni -1, 2 dan 5. Coba saja anda mencari nilai x=0 di persamaan awal, maka anda akan mendapatkan hasil +88, dan seterusnya..

Sekian dari saya, apabila banyak kekurangan dan kesalahan mohon dimaafkan, Wassalamu'alaikum!

#nb: komentari yang salah karena kita masih sama-sama belajar terimakasih :D

Limit Trigonometri (X->0) (0/0)

Assalamu'alaikum !

Pada postingan kali ini, kita akan membahas tentang Limit Trigonometri X mendekati 0 dan Kontinuitas.

hmm jadi gini...

Gambar di atas:Karena X mendekati 0 yang menghasilkan nilai 0/0, kita harus mencari bentuk lain, seperti sin x / x= 1, sehingga nilai 0 tidak perlu kita subtitusikan (jika menghasilkan 0/0).

Pada Kontinuitas, step 1 / langkah 1 kita hanya perlu melihat persamaan dimana x >= ataupun x<= c. ya, kita cukup melihat >= atau <=.


Pada step ke 2, limit x mendekati c, ada simbiol + dan - kecil di bagian kanan atas angka tersebut, itu berfungsi untuk memnentukan dia sebelah kana  atau kiri.

sehingga, pada limit x mendekati 1 simbol(-) maka persamaannya yaitu 2x, karena pada 2x, syaratnya adalah x < 1 (sebelah kiri). sedangkan limit x mendekati 1 simbol (+) maka persamaannya yaitu x^2+1, yang dimana syaratnya adalah X>=1 (sebelah kanan).

pada step ke 3, kita hanya melihat apakah ada perbedaan hasil antara f(x) dengan f(a), jika tidak, maka fungsi tersebut kontinu pada x = c, jika tidak, maka ia tidak kontinu / diskontinu.







 
Pada nomor 3, stepnya tetap sama, hanya sedikit berbeda pada pembagian pengerjaan.
pada soal tersebut, terdapat x bernilai -3 dan 3. sehingga kita mengerjakannya masing-masing.


setelah didapatkan hasilnya masing-masing, eliminasilah untuk mencari nilai a dan b nya.

Semoga mudah dipahami sekian dari saya, mohon maaf bila banyak kekurangan dan kesalahan
Sekian Wassalamu'alaikum!

#Komentari apabila ada kesalahan, kita sama-sama belajar :D.

Limit Fungsi

Assalamu'alaikum !

Bahas Limit Fungsi Yuks!

Sifat-sifatnya dulu dong,

1. lim k = k
    x-->c

2. lim x = c
    x-->c

3. Jika lim f(x) dan lim g(x) ada, dan k elemen Real
            x-->c                       x-->c
      maka:


gambar diatas masih sifat yaa...

Contoh soal dan pengerjaannya,



Limit bilangan e





Video bisa disimak untuk lebih jelasnya pada link berikut
Link : (coming soon)

Sekian materi singkat yang dapat saya bagi, sayapun masih sedang belajar dan masih sangat banyak kekurangan, bila ada kesalahan ataupun pertanyaan, silahkan dikomentari agar sayapun dapat memperbaiki dan mempelajari pertanyaan untuk kemudian dijawab bersama-sama.

Wassalamu'alaikum Warahmatullahi Wabarakatuh.
Semoga Bermanfaat untuk teman-teman semua :))

Fungsi dan Grafik

Assalamu'alaikum !

Postingan ini akan membahas Fungsi

Fungsi dalam istilah matematika merupakan pemetaan setiap anggota sebuah himpunan (dinamakan sebagai domain) kepada anggota himpunan yang lain (dinamakan sebagai kodomain). Istilah ini berbeda pengertiannya dengan kata yang sama yang dipakai sehari-hari, seperti “alatnya berfungsi dengan baik.” Konsep fungsi adalah salah satu konsep dasar dari matematika dan setiap ilmu kuantitatif. Istilah "fungsi", "pemetaan", "peta", "transformasi", dan "operator" biasanya dipakai secara sinonim.
(Source:Wikipedia, https://id.wikipedia.org/wiki/Fungsi_(matematika))

Pada gambar dibawah ini, contoh dari fungsi



Jadi intinya, Fungsi itu terdiri dari Domain (asal/sebelah kiri) dan CoDomain (Tujuan/sebelah kanan).

Untuk Domain,
Domain Harus mempunyai Pasangan (Tidak boleh Jomblo)
Domain Tidak boleh Selingkuh / Poligami (Hanya boleh 1 pasangan)
Domain Harus seluruhnya Punya pasangan, tidak boleh ada 1 Domain yang jomblo

Untuk CoDomain
CoDomain Boleh di Poligami (Pasangan lebih dari 1)
CoDomain Boleh Tidak punya pasangan (Boleh Jomblo)

Itu beberapa syarat agar dapat dinyatakan sebagai FUNGSI.

Fugsi juga terbagi beberapa sifat, yaitu:
1. Fungsi Injektif
2. Fungsi Surjektif
3. Fungsi Bijektif
4. Fungsi Komposisi

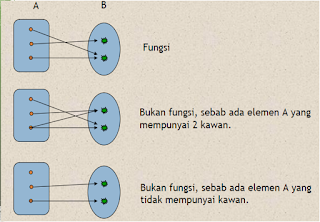
1. Fungsi Injektif atau Onto atau Fungsi satu ke satu
    Jika X1 tidak boleh = X2 => f(x1) tidak boleh = f(x2)
    Jika x1 = x2 => f(x1) = f(x2)
    Setiap Doamain harus terisi penuh dan tidak selingkuh,
    CoDomain Tidak harus semua terisi

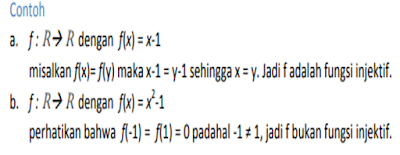
2. Fungsi Surjektif (Pada atau Onto)
    Maksudnya itu setiap Domain memasangkan satu CoDomain (tidak ada CoDomain yang Poligami      / 2 pasaang/lebih)
    Setiap Domain harus mempunya pasangan
    CoDomain boleh poligami/pasangan lebih dari 1.


3. Fungsi Bijektif (Koresponden satu ke satu) (Gabungan)
    Gabungan antara Injektif dan Surjektif
    -Domain tetap wajib punya pasangan
    -CoDomain Tidak ada yg Jomblo
    -CoDomain Berkoresponden satu ke satu (Tidak menyilang)



4. Fungsi Komposisi

Df yaitu Domain f, Rg itu Range g.




Grafik Fungsi

Grafik Fungsi adalah grafik yang memunjukkan hubungan antara setiap nilai x dengan bayangannya (y) pada suatu fungsi f.



a. Fungsi Linear
    f(x) = ax + b
    Grafik ini akan berupa garis lurus

b. Fungsi Kuadrat



penjelasan materi ini lebih lanjut akan dilanjutkan di youtube:
Link: (comingsoon).


Sekian materi singkat yang dapat saya bagi, sayapun masih sedang belajar dan masih sangat banyak kekurangan, bila ada kesalahan ataupun pertanyaan, silahkan dikomentari agar sayapun dapat memperbaiki dan mempelajari pertanyaan untuk kemudian dijawab bersama-sama.

Wassalamu'alaikum Warahmatullahi Wabarakatuh.
Semoga Bermanfaat untuk teman-teman semua :))

Nilai Mutlak

Assalamu'alaikum !

Pada postingan kali ini, saya akan sedikit mencolek materi tentang nilai mutlak
Cuss aja yuk!

Mulai dari sifatnya dulu,

Sifat Harga Mutlak


Contoh Soal



untuk mencari ++ atau -- nya, lihat pada nilai X1 dan X2, diantara nilai tersebut terdapat angka 0, sehingga kita bisa memasukkan angka 0 sebagai perwakilan (bisa angka -2,-1,0,1/4,...) untuk mempermudah mencari ++ dan -- nya.

Kita masukkan angka 0 pada persamaan kuadrat yang akan difaktorkan, sehingga 3(0)^2+8(0)-2>=0
dan kita mendapatkan hasil -2, cukup ambil -- nya saja, sehingga diantara nilai X1 dan X2 adalah -- (negatif), sisanya positif (ada pola + - + -).

setelah itu, untuk menentukan arah nilai X nya, kita lihat pada persamaan kuadrat yang akan difaktorkan, dia bernilai >= (besar dari sama dengan) 0 (nol), sehingga karena >=0, itu bernilai ++ (positif), lalu kita tari garis dari titik nilai X tersebut menuju area positif.

Untuk lingkaran tebal pada masing-masing X, dikarenakan bertanda >= (besar dari sama dengan) ataupun (kecil dari sama dengan), itu ditebalkan titiknya, sedangkan untuk X yg bertanda > (besar dari) ataupun < (kecil dari), titiknya hanya bulat atau lingkaran kosong, tidak ditebalkan.

Sehingga didapatlah Himpunan penyelesaiannya yaitu X<=-3 atau X>=1/3.

Sekian materi singkat yang dapat saya bagi, sayapun masih sedang belajar dan masih sangat banyak kekurangan, bila ada kesalahan ataupun pertanyaan, silahkan dikomentari agar sayapun dapat memperbaiki dan mempelajari pertanyaan untuk kemudian dijawab bersama-sama.

link pembahasan : (coming soon)

Wassalamu'alaikum Warahmatullahi Wabarakatuh.
Semoga Bermanfaat untuk teman-teman semua :))

Pertidaksamaan Bilangan Real

Assalamu'alaikum Wr. Wb.

Pada Postingan kali ini, saya akan berbagi materi yang saya dapatkan yaitu pertidaksamaan bilangan real.

Apa itu Bilangan Real?

penjelasan itu ada dipostingan sebelum postingan ini :D.

Langsung saja cusss!

Apa itu Pertidaksamaan? Pertidaksamaan adalah himpunan bilangan yang memenuhi sifat urutan bilangan tertentu yang dinyatakan dalam salah satu lambang, > Besar dari, ³Besar dari/sama dengan, £ Kurang dari/sama dengan, < Kurang dari.

Maksud dari  simbol ³ dan £ yaitu nilai suatu X dimulai PAS dari nilai a hingga seterusnya ( besar dari berarti ke kanan, dan sebaliknya ). Kita dapat mengetahui maskudnya jika melihat garis bilangan yang ada pada video saya pada link berikut:

Pertidaksamaan Bilangan Real (Soal+Pengerjaan)

Contoh:

Jika diketahui nilai a = 3, dan b = 2.

maka

   a > b (a lebih besar dari b)

   b < a (b lebih kecil dari a)

Coba Kerjakan soal Berikut:

Jika sudah, cek jawabannya pada link Pertidaksamaan Bilangan Real (Soal+Pengerjaan).

Sekian yang dapat saya bagi, segala kekurangannya mohon dimaafkan, jika ada pertanyaan silahkan pada kolom komentar.

Wassalamu'alaikum Wr.Wb.

Jenis Jenis Bilangan

Assalamu'alaikum Wr.Wb.

Pada postingan kali ini, saya ingin berbagi materi beberapa macam bilangan, mulai dari Bilangan Riil/Real, Bilangan Asli, Bilangan Cacah, Bilangan kompleks, Bilangan Bulat, Dan Bilangan Imajiner.

1. Bilangan Riil / Real, dalam matematika dapat dituliskan dalam bentuk Desimal,
seperti 4,123887... atau 3,25678. Bilangan Real/Riil ini meliputi Bilangan Rasional seperti 12 ataupun -33/11, dan Bilangan Irasional seperti  Phi ataupun akar 2.

2. Bilangan Rasional, yaitu bilangan yang dapat dinyatakan dalam p dan q, dimana p,q ϵ bilangan bulat, jika dinyatakan ke bentuk p/q maka q ≠ 0. Contohnya: 3/11, 5, -5.....

3. Bilangan Irasional, yaitu bilangan yang tidak dapat dinyatakan p atau q. Contohnya: log 2, e, √7, i.

4. Bilangan Cacah, terdiri dari {0,1,2,3,4..}.

5. Bilangan Bulat, yaitu terdiri dari bilangan cacah {0,1,2,3,4..} dan bilangan negatif {-1,-2,-3,..}.

6. Bilangan Asli, yaitu bilangan bulat positif namun 0 tidak termasuk, {1,2,3,4..}. Ada juga pendapat dari logikawan dan ilmuan komputer, mengatakan 0 dan bilangan  bulat positif yaitu bilangan asli,
{0,1,2,3,4...}.

7. Bilangan imajiner

8. Bilangan Prima, yaitu bilangan yang tidak dapat dibagi kecuali dirinya sendiri, Contoh: {1,2,3,5,7,11,13,17,....}

9. Bilangan Kompleks

Itulah beberapa materi yang semoga dapat dipahami dan bermanfaat untuk kita semua, jika ada kesalahan mohon dimaafkan, sekian dari saya, Wassalamu'alaikum Wr.Wb.

Source: Wikipedia.